
創作してみよう
折り紙の創作には様々なパターンがあります。
例えば、適当に折ってたものが「何かエイリアンに見えた!」とかでも立派な作品です。
さらにシンプル作品では、次に書くような創作法や理論を使わないものがほとんどです。
なので自分の好きな方法で創作してもらうのが一番なのですが、急に「創作して」と言われても困ると思うので、まずは基本形を使った創作法を載せておきます。
作りたいものとカドの数を決めよう
1・作りたいものを決める
まずは何はともあれ折りたいもの、モデルを決めましょう。
筆者はモンハンのモンスターが折りたかったため創作を始めました。
好きなものを選ぶのがよいですが、できれば一つほど特徴のあるものがGOOD。
2・モデルの特徴とバランスつかむ
折りたいものは決まりましたか?
では、そのモデルの特徴的な部分はどんな形をしていますか?
物によってはその特徴的な部分だけでモデルが何かわかると思います。
また、手足や頭などの大きさ、バランスはどうなっているでしょうか。
これらの特徴をしっかりと把握するためには、一度スケッチをしてみましょう。
このとき、作品の一番見てほしい方向も決めます。
創作初心者の場合、全方位から見られるような作品を作るのは難しいからです。
例えば、サカナを創作したいなら横から見た形が最もなじみ深いでしょう、逆に上下から見た形はあまり見覚えがなく、特徴もつかみづらいでしょう。
つまり横から見ることを意識した創作をするのが無難です。
そして見る方向を決めたらその方向からのスケッチを描いてみましょう。
特徴やバランスがよく把握できると思います。
3・カドの数を決める
次は大まかにカドの数と大きさを決めましょう。
例えば、トカゲなら前足が一対、後ろ足が一対と頭と尻尾の6つのカド。
このうち尻尾が大きくあとは小さいカドが必要です。
タコなら足が8本、頭が1つで9つのカドが必要です。
頭も足も同じくらいの大きさのカドが必要です。
ここで大まかなカドの数と大きさを計算し、どの基本形を使うかを決めます。
出来れば樹系図にもまとめてみましょう。
4・どの基本形を使うか選ぶ
次にいよいよ基本形を選んでいきます。しかしまずは基本形を知らないとお話になりません。
そこでこちらに有名な基本形とそのカドの数を載せておきます。
展開図のみなので、もし展開図折りがわからない場合は創作法の展開図折りの項をご覧ください。
さて、ではどように基本形を選べばよいのでしょう。
それは…野生の勘!
で選んでもよいのですが、最も重要な基準は、
カドの数と大きさです。
例えば先ほど言ったようにトカゲは6つのカドを必要とします。
カド6つといえば…そう「ブタの基本形」です!
カドの数が同じ、もしくはカドが多い基本形を選びましょう(必要より多いカドは使わなければいいので)。
また、カドが9つのタコの場合はどうでしょう。
実はタコの場合は四鶴が最も良いと考えられるのですが、なぜでしょう。
9つのカドなら、アヤメの基本形も大きいカドと小さいカドをあわせて9つあります。
しかし、アヤメの基本形は四鶴と比べてタコの創作に向きません。

ブタの基本形
トカゲに向いてる
アヤメの基本形
四鶴


大きいカド:5つ
小さいカド:4つ
大きいカド:9つ
小さいカド:4つ
タコ向き
5・試し折りをしよう
次は試し折りをしてみましょう。
実際に選んだ基本形を折り、自分なりに仕上げてモデルに近づけてみましょう。
どうでしょうか、自分の納得のいく作品になったでしょうか。
もし、完成したのなら、おめでとうございます。
しかし、納得できる作品ができなかった人も多いでしょう。
ではどこが納得できませんでしたか?
ここでどこができなかったのかしっかり把握しておきます。
それによって次のステップが変わります。
ではまずカドの数や大きさが足りていない場合は基本形を選びなおす、または基本形を組み合わせてみましょう。
カドは足りているが特徴ができていない場合は部分折りをしてみましょう。
基本形では満足できなかったあなた、基本形そのままでは望みのカドの数とバランスにならないことも多いと思います。
そこで基本形の改造をやってみたいと思います。
「え、基本形を勝手に改造とかしていいの?」とお思いのかた、残念、もうあなたは組み合わせています。
例えば、四鶴は鶴の基本形を4つ組み合わせた基本形ですし、アヤメの基本形はサカナの基本形を4つ組み合わせたものです。
このように正方形を4分割し、基本形を4つ組み合わせ自分だけの基本形を作り上げましょう!
6・基本形を組み合わせよう
四鶴
アヤメの基本形




基本形の
組み合わせ
円領域を理解しよう
さて基本形の組み合わせまで学んできたわけですが、このままでは組み合わせた基本形のカド数や大きさがいちいち試し折りしなくて把握できません。
もちろん片っ端から試し折りして作ってゆくのもよいですが、展開図からカドの数や大きさが予測できれば便利ですよね。
そこで考える理論が円領域です。
円領域とはカドの大きさや数を円の形で示す理論です。
まあ言葉で言っても伝わりづらいので右の図をご覧ください。
鶴の基本形は大きなカドが4つと小さいカドが1つありますが、右図の鶴の基本形の展開図に大きい円が4つと小さい円が1つ重ならずきれいに収まっているのが分かると思います。
ちなみに円は外にはみ出していても、中心が展開図に入っていればOK、右図では円が4分の1しか入っていませんが中心が展開図に入っているのでOKです。
しかし、いまいち理解できていないそこの方、その辺のティッシュを一枚お手に取って、真ん中からこよりを作ってみてください。
そして広げてください。
すると、ティッシュの真ん中に円形にしわが入っているのがわかるでしょう。
これが円領域です。
このように円領域とは展開図のカドの部分を円で表しカドの数と大きさを把握しやすくしてくれます。
次にどうやって展開図に円を示したらよいか説明します。
ずばり鋭角が集まっている部分です。
さてそこを中心に円を広げていくと、接線になるような線があると思います。
そこまで円を広げたらOKです。
基本形を組み合わせ、円領域を使ってカドの数と大きさを推定し、自分好みの基本形を組み合わせましょう。

大、1
鶴の基本形
大、2
大、4
大、3
大きいカドが4つ、小さいカドが1つあることが分かる。
円の4分の3が展開図からはみ出ているが、中心が入っているのでセーフ

「鶴ドラゴン」は本来基本形ではなく、四隅から大きいカドを4つ、内部から小さいカド4つ折り出すことを言う。

基本形の組み合わせは確かに様々な形が作れますが、カドの大きさのバランスが取りづらいと思います。
そこで「付加」という手法を使います。
例えば右の展開図を見てください。
ピンクの部分を合わせると鶴の基本形になります。
つまり、鶴の基本形の真ん中に蛇腹が「付加」されています。
次に下の図を見てみると、鶴の基本形の二辺に蛇腹が「付加」されています。
さて、ここまでで気づいた方はいますでしょうか。
「付加」した部分を取り除いても正方形になります。
つまり、正方形の形を保ったまま様々な構造をくっつけることができるということです。
では、実際に折ってみましょう。
まず、対角線上に蛇腹を折ってみましょう。
蛇腹の幅や、数は適当で。

7・基本形に付加してみよう
蛇腹付加1
合わせて
正方形になる
蛇腹付加2
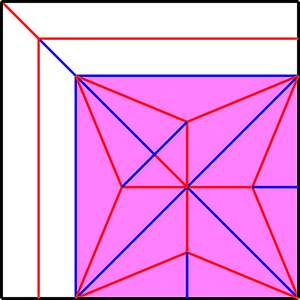
対角線蛇腹付加

このまま
鶴を折る
出っ張っている部分はありますが正方形になります。
これでそのまま鶴を折ってみましょう。

頭と尻尾が長い
頭と尻尾の
円領域が大きい

すると鶴の頭と尻尾が長くなっています。
これは円領域で考えると分かりやすいですが、頭の部分と尻尾の部分の円が大きくなっています。
つまり蛇腹を付加すると付加した部分に領域が増えるので円が大きくなり、カドが大きくなります。
またこちらに書く横分子蛇腹法という理論を使うことでさらに様々な構造を作ることができます。
このように正方形が残るように蛇腹を入れることによってカドの数や大きさの調節ができます。
また、蛇腹ではないですが、座布団折りをしてから折ることでも様々な構造を加えることができます。
これらの付加を使いこなし、創作に必要な大きさと数のカドを折りだしましょう!
座布団小鳥

8・部分折りしよう
創作では多くの試作を繰り返し行います。
しかし、作品の一部だけを変えたいときにいちいち全身を試作していては時間がかかります。
そこで作品の一部だけ試作します。
これを部分折りと呼びます。
では一例を示してみましょう。
ドラゴンを作りたくて、鶴ドラゴンに対角蛇腹を付加して右のような展開図を作りました。
しかし頭部分の構造がまだ決まっていません。
そこで頭を部分折りしてみます。
ピンクの部分が頭になるので、この部分だけをまず折ります。
ここからは好きに折ってもらうわけですが、注意してほしいのは緑で示した部分だけは変えてはいけないということです。
要するに体との接続部分ですが、ここが変わってしまうと合わなくなってしまいます。
逆に言えば緑の部分以外はどのように折ってもよいということなので、好きなだけこねくり回しましょう!
もし接続部分を変更したい場合は、もうちょっと部分折りの範囲を大きくするか、全体の基本形を見直しましょう。
こちらに部分折りの例も示しておきます。
展開図のみなので少々わかりにくいですが、手足の爪や、頭部の角などを作りたい場合などに活用してみてください。
正方形
対角線蛇腹付加鶴
頭
尻尾
羽
羽
足


接続部分は
変わっていない
基本形を使って大まかに折ろう
細部を作りこんでいこう
10・まとめ
これが私がよく使う創作の流れです。
しかし初めて創作に挑む場合、いきなり展開図やらを作るのは難しいと思います。
そんなときは実際紙を手に何度も折ってみましょう。
正直なところ折り紙をホームページだけで伝えるのは無理です。
多くは実際に折り紙を折ってもらい、自身で知識を深めてもらうきっかけや、行き詰ったときのヒントになればよいと思います。
9・試し折りをしよう
ここまででできた展開図で一度試し折りしてみましょう。
創作は展開図→試し折り→改善点を見つける→展開図を改善、と試し折りと展開図の改善を繰り返し完成に近づけていきます。
試し折りはできればどんどんしていきましょう。

「これは…あの、あれや、蒲焼きさん太郎や!」
といえば、
誰が何と言おうがこれはもう蒲焼きさん太郎なのです。



上から見た
アリのスケッチ
小、1
タコ向きじゃない
これはアヤメの基本形と四鶴を実際折ってみればわかりやすいと思いますが、実はカドの大きさが違います。
タコの場合9つのカドのうち、8本は足で同じ大きさのカドが必要になります。
アヤメの基本形を見てみると、大きいカドが5つで、残りは小さいカドしかありません。
一方四鶴には大きいカドが9つあり、タコの足を折るのに十分なカドがあります。
つまり、基本形はカドの数と大きさが十分なものを選ぶのが良いということです。

さてここで、一つ例を考えてみます。
右図のように、展開図に円領域を示しました。
すると円と円の間に一定の幅の隙間ができました。
これを帯領域と呼びます。
帯領域はカドではなく、複数のカドの幹の部分を表します。
今までの円領域ではカドの根元はすべて同じ部分になります。
しかし、カニのはさみのように先の部分だけカドが分かれている構造では幹の部分が必要です。
この幹の部分が展開図で帯領域として表されます。
帯領域は複数の円領域を囲むようにできます。
そして囲まれた円領域のカドが先の枝分かれとなり、帯領域がその根元の幹になります。
つまり下の樹系図ような構造は右の円領域の例で作ることができるということになります。
また帯領域は必ず一定の幅で紙の端までつながる、または一周しなくてはなりません。


右の円領域から
予想される樹系図
帯領域と円領域の例


トカゲの樹系図
タコの樹系図

蛇腹系の展開図折りをしよう
22.5度系の展開図折りをしよう
展開図の通りに折り筋をつけるには、次の4つの方法を把握することです。
まず角の二等分線。
2本の線やを合わせるように折る。
最も基本的な折り筋の付け方で、紙の淵に合わせて折るなど、はこの操作である。展開図折りでは段折りを使わなければならない場合が多い。
次に垂直二等分線
これも基本的な折り筋の付け方。紙の角と点を合わせて折る、のはこの操作。展開図折りでは紙の角を点に合わせる他、段折りのように折る場合もある。
次にある点を通る垂線。
こちらは同じ直線を重ねるように折ります。ある点から垂線を引くことも出来る。
最後に点と点を結ぶ線です。
折り紙ではこの折り筋の付け方が難しく、間違えやすい。どの点同士を結ぶか鉛筆等で印を付けておくのがよい。
これら4つが基本的な折り筋の付け方です。
ここまでで気付いた方も居るかもしれません。
そう!これらは全て作図と同じなのです。
折り筋の付け方、順番がわからない場合はまず作図で展開図が描けるか試してみましょう。
・プリントせずに折るには
展開図を作図で描いてみる
折り筋をつけてみましょう、と言いましたが、図の通りにできたでしょうか。
できないという方は右の図をプリントして、折ってみましょう!
・折り筋の付け方がわからない方は…
展開図折りする場合まず何をするかというと、
ずばり、折り筋をつけます。
何事も折り筋をつけないと始まらないのです。
そこで右図の展開図の通りに折り筋をつけてみましょう。
・まずは折り筋をつけよう

展開図折りはできたでしょうか、できる方は問題ありませんがもちろん「いきなりできるかっ!」ていう方もいると思います。
出来なかった方はまずは一度折ったことのある作品を展開図折りしてみましょう。
今回はおそらくみなさん折ったことのある「鶴」を展開図折りしてみます。
折ったことのある作品に挑戦しよう
展開図折りに挑戦してみよう
展開図折りに挑戦
赤:山折り
青:谷折り





角の二等分(1)
角の二等分(2)
垂直二等分
点と点を結ぶ
ある点を通る垂線
折り筋がすべてつけ終われば次はいよいよ折りたたんでいきます。
折り図では明確に折り方や順番が示されていました。
展開図折りでは好きに折ってもらってかまいませんが、やはり折りやすい順番というものがあります。
それは難しい部分から折るというものです。
つまり、最も折りにくい紙の中央部分から折り始めることが大事です。
折り図でも多くは中央部分から折り始めています。
今回鶴では中央(背中部分)のカドから折り始めましょう。
後は折り筋の通りに折りたたんでいくのみです。
折りたたむには
ここまでで鶴の基本形が出来上がっていると思います。
実は展開図ではここまでの情報しかありません。
したがってここからは完成写真を見ながら、近づけていくということになります。
鶴の基本形には大きいカドが4つと小さいカドが1つあります。
これらのカドが完成のどの部分にあたるのか、それぞれ決めていきます。
今回は展開図にそれぞれの部位を示したのでこれを参考にしてください。
あとは写真をよく見てどこを折り返しているのか、頭の大きさどれくらいか、などを判断し、折って下さい。
できなければ折り図なども参考にして折りましょう。

腹ビレ
胸ビレ
頭
胸ビレ
背ビレ
腹ビレ
尾ビレ
尾ビレ
仕上げ


羽
背中
頭or尻尾
羽
頭or尻尾


ここから折る
横分子蛇腹法を使った作品の展開図折りは他とは少々異なり、まず縦横(または各対角線)にn等分の蛇腹を折る必要があります。
そして、できたマス目に沿って折り筋をつけていきます。
折り筋の段階で非常に間違えやすいので注意しましょう。
今回のトカゲは16等分なので、まず縦横に16等分の蛇腹を折ってから始めます。


前足
後ろ足
尻尾
頭
前足
後ろ足
トビウオ
トカゲ

展開図を折りたたんだ図
折り筋をつけた後は折り筋の通りに折れば畳めるはずなので、何度かチャレンジしてみましょう。
仕上げに関してははっきりとわからないのが普通です。
無理やりでもよいので完成に近づけましょう。


山谷ついた展開図が
おすすめ


まず16等分する
折り紙初心者のための手ほどき
折り図(折り方の本)を見て折れない人向け
折り紙中級者のための手ほどき
折り図を見て折れるが、うまく仕上がらない人向け
折り紙上級者のための手ほどき
展開図折りや創作を始めたい人向け
折り紙上級者のための手ほどき
創作を始めたい人向け
折り紙創作者者のための手ほどき
本格的に創作を始めたい人向け
基本形の一覧や、理論などのまとめ


