部分折りの一例を記載。
創作法と合わせてご覧ください。
横分子蛇腹法(通称、蛇腹)についての記載。
創作法と合わせてご覧ください。
基本的な折り紙の手法について記載。
折り方のコツと合わせてご覧ください。
基本形一覧
サカナの基本形

大きいカドの数:2
小さいカドの数:2
アヤメの基本形

大きいカドの数:5
小さいカドの数:4
鶴の基本形

大きいカドの数:4
小さいカドの数:1
四鶴

大きいカドの数:9
小さいカドの数:4
鶴ドラゴン

大きいカドの数:4
小さいカドの数:4
ブタの基本形

カドの数:6
小鳥の基本形

大きいカドの数:1
小さいカドの数:3
座布団小鳥

大きいカドの数:1
小さいカドの数:3
横分子蛇腹法
横分子蛇腹法とは創作法の一つで、蛇腹折りを用い「好きな大きさのカドを好きなだけ折りだす」ための理論で、とても便利な創作法です。横分子蛇腹法を使いこなすには、まず円領域と横分子を学びましょう。
円領域についてはこちらをご覧ください。
横分子とは
横分子とはカドの付け根をカドに対し垂直方向にぶった切った場合にできる分子です(図1)。
横分子はカドが使用している紙の部分そのものである。
つまり必要な大きさの横分子を配置して、川崎定理、前川定理を満たすように展開図を作っていけば、任意の数と大きさのカドを作り出すことができます。
川崎定理、前川定理とは平面に畳める展開図の条件を示しています。
これらの条件を満たさないと平面に折りたためません。
しかし、横分子の形は様々であり、これらを折り畳めるように配置することは非常に難しいです。
そこで使われる方法が横分子蛇腹法です。
横分子蛇腹法での横分子
横分子蛇腹法は横分子の形を制限することで横分子の配置をしやすくする方法です。
では、その形は何かというと、正方形です。
正方形の横分子は図2の通り非常にシンプルです。
この分子をこれから説明する4つの条件を満たすように配置することで、川崎定理、前川定理を満たし、任意の数と大きさのカドを作り出せるようにしていきます。


図1 鶴の基本形とその横分子

図2 正方形の横分子



条件1 蛇腹のグリッドに合わせよう
横分子蛇腹法は文字通り、横分子と蛇腹を組み合わせた方法です。
しかし、ここでいう蛇腹とはただ平行に山折りと谷折りをつけただけのものではなく、グリッドになるように折り筋をつけることです。
横分子蛇腹法では基本的に図3のように縦と横に正方形のマス目になるように蛇腹を折る必要があります。
そして正方形の分子をグリッドに合わせて配置します。
ここで、横分子の例をいくつか見てみましょう。
まず、最小の1マスの大きさのカドは2×2マスの分子になります(図4)。
次に2マスのカドは4×4マスの分子になります(図5)。
さらに3マスのカドは6×6マスの分子になります(図6)。
4マスのカドも、5マスのカドも同様に分子が大きくなっていきます。
このようにグリッドに合わせた正方形の分子をグリッドに合わせて展開図に配置することが、一つ目の条件です。

グリッドになるように
折った蛇腹
図4 1マ�スカドと分子
図5 2マスカドと分子
図6 3マスカドと分子
条件2 45度線を繋げよう
では具体例を用いて展開図を作ってみましょう。
4×4マスの蛇腹(グリッド)から2マスカドを2つ、1マスカドを2つ折るための展開図を考えていきます。
そこで条件1を使い、図7のような展開図を作りました。
ちなみに横分子は円領域と同様に中心さえ入っていればよいので、図7のように一部はみ出していてもOK。
さて、この展開図は折れるでしょうか。実際折ってみると分かりますが、折れません。
なぜなら45度線が途中で途切れているからです。
45度線とは横分子蛇腹法では、蛇腹に対して45度の角度になる線のことです。
この45度線が繋がるように配置すると図8になります。
つまり、横分子から出てくる45度線を紙の端まで繋げるか、環状に繋げなくてはなりません。
このとき条件4を満たせば分子以外の部分でどのように繋げても構いません。

図7 条件1を満たすが失敗例

図8 条件1,2を満たす正解例
条件3 カドの中心を谷折りと谷折りの交点に合わせる
条件2の例で、図9のような展開図も考えられると思います。
45度線は全て繋がっています。
しかし、図9の展開図は折れません。
なぜかというと、分子の中心が谷折りと谷折りの交点になっていないからです。
図9では1マスカドの中心が山折りと山折りの交点になっています。
これでは前川定理が満たせず、折れません。
実は横分子の中心は谷折りと谷折りの交点に限定されてしまうのです。
ちなみに山折りと山折りの交点は裏から見ると谷折りと谷折りの交点になり、裏側にカドを折りだせます(図10)。
このときカドが裏面の色になるので注意。
逆に言えばインサイドアウトを使う場合はこの技術も存分に活用しましょう。

図9 条件1,2を満たすが失敗例
分子の端では45度線を曲げる
最後の条件は少しややこしいです。
やはり条件2の例を考えてみましょう。
図11は条件1~3をすべて満たしています。
しかし、2マスカドが2つ、1マスカドが2つになりません。
よく見ると分かりますが、2マスカドが4つできてしまいます。
2マスカドは段折りで1マスカドにできますが、これでは分厚くなってしまったり、新たに糊付けが必要になったりと欠点も多いです。
そこで、カドは必要以上に大きくしないために次の条件を満たしましょう。
45度線を分子の端で曲げるということです。
45度線を曲げずに伸ばすと、他の分子にぶつからない限りカド(分子)が大きくなる、または帯領域ができてしまいます。
図12では45度線が分子の端で全て曲がっています(1マスカドが3つになってしまいましたが)。

図10 条件1-3を満たす成功例

図11 条件1-3を満たすが失敗例

図12 条件1-4を満たす成功例
これらの4つの条件を満たすように自分の好きな大きさのカドを好きなだけ配置することができれば、もう横分子蛇腹法は半分マスターしたといってよいでしょう。
しかし、最小限の条件を与えられただけでできる人は少ないと思います。
そこでいくつか例題を解いてみましょう。
その中でどのようにカドを配置し、組み合わせればよいかを学んでいきましょう。
例題1
8等分蛇腹で4マスカド2つと2マスカド3つを作りなさい
例題2
8等分蛇腹で4マスカド1つと2マスカド5つを作りなさい
例題3
16等分蛇腹で8マスカド1つと6マスカド1つ、4マスカド2つ、2マスカド2つを作りなさい
例題1解答例
まず大きいカドの4マスカドは紙の隅に配置する方が効率が良いです。
なぜなら分子の中心が紙に入っていればよいからです。
大きいカドを紙の中央に配置すると、分子全体が紙を占領してしまうため、非常に邪魔です。
よってできるだけ、カドは紙の端、特に大きいカドは隅に配置するようにしましょう。

例題2解答例


例題3解答例

帯領域
ここでまた一つ例を考えてみます。
人型を作るため、右のような樹形図を考えました。
頭と腕になる2マスカドが3つと足になる4マスカドが2つあります。
これらを折りだすため、図13の展開図を作りました。
では実際折ってみるとどうなるでしょう。
折ってみると、図14の樹形図のように胴体のない形になりました。
このような場合どうすればよいでしょうか。


図13 人型の展開図、失敗例
カドの根元がすべて同じ位置にある

図14 人型の樹形図、失敗例
ここで必要になるのが「帯領域」です。
円領域の項でも解説しましたが、折り紙の造形には「カド」以外にも幹となる部分「帯領域」があります。
これは上記のような胴体部分やカニの腕などの造形を作る場合に必要になります。
帯領域がないと図14のようにカドはすべて同じ根元から生えます。
円領域では、複数の円を囲むように一定幅の帯領域ができます。
横分子蛇腹法でも同様に複数に横分子を一定幅で囲むことで帯領域ができます。
そこで図15の展開図を考えました。
この展開図では2マスカド3つが2マス幅の帯領域に囲まれています。
これにより、2マス分の「幹」の先に2マスカドの3つの枝分かれができ、人らしくなりました。
これが「帯領域」の力なのです。
また、帯領域も一部が紙の外にはみ出ていても問題ありません。
このように枝分かれになるカドを幹となる帯領域で囲むことでより自由に造形ができるようになります。
任意の大きさのカドと帯領域を組み合わせ、思い通りの創作を楽しんでみてください。


カドの根元が胴体の分ずれている
図16 人型樹形図、成功例
図15 人型展開図、成功例
例題4
下の展開図を折りたたんだ場合の樹形図を書きなさい。
(1)

(2)

(3)

例題4解答
(1)
(2)

(3)


部分折りの例
22.5度系



対角蛇腹



二辺蛇腹


辺-22.5度系


辺-蛇腹


基本の折り方
かぶせ折り、中割り折り、段折り
右図の工程まで鶴を折って下さい。
この鶴を基本としてこの項を説明します。
何個も折るのはめんどいと思うので、鶴は使いまわしてください。
この後は頭の部分を折り曲げて完成です。
通常は(1)のように中割り折りをします。
しかし、中割り折り以外にも折り曲げる方法がいくつかあります。
この項では折り紙の基本である中割り折り、かぶせ折り、両側で段折り、二段中割り折りを学びその折り方とその性質を学びましょう。


(1)中割り折り
中割り折りはカドを開いている方向に曲げることができます。
このとき折れ曲がる部分は角が取れており、緩やかに曲がります。
ではほかの折り方ではどうでしょう
こちら側が開いている
閉じている
角が取れている
(2)かぶせ折り

次はかぶせ折りです。
カドが閉じている方向に曲がります。
また、折れ曲がる部分の角が取れています。
中割り折りとかぶせ折りは似ていますが、まったく逆の方向に曲がるという性質を持っています。
(3)両側で段折り


(4)二段中割り折り
そして折り図でよく目にするであろう「両側で段折り」です。
これは開いている方向に折れ曲がるため、中割り折りと似た性質ですが、折れ曲がる部分の角が取れません。そのため鋭利に折れ曲がることができます。
角が取れていない
最後に二段中割り折りです。
その名の通り二回中割り折りを行います。
しかし、通常の中割り折りと比べるとまったく異なる性質を示します。
曲がる方向は逆方向になり、折れ曲がる部分の角は取れていません。

中割り折り
角�が取れている
これらの性質まで覚える必要はありませんが、折り図の通りに折れないときにこの4種の折り曲げ方を使ってみてください。
もしかするとかぶせ折りと中割り折りを勘違いしていたりするかもしれません。
沈め折り
次は「沈め折り」、主にカドを細くするための手法です。
折り紙の手法の中では最難関と言われています(言われてなくても私が言います)。
では沈め折りの最もシンプルな例を折ってみましょう。

このように沈め折りはカドをつぶしたりするほか、カドを細くしたりするのに必須のテクニックです。
できない方は一度思い切って大きく開いてしまうのが、コツです。
紙の裏からも手を突っ込んで折りましょう。
さて、実は沈め折りにはopen sink と closed sink の二種類あることはご存知でしょうか。
これら二つは折る操作が異なるだけでなく、完成形にも大きく影響することがあります。
ここでそれぞれの性質を書いておきます。
Open sink はその名の通り紙を大きく開いてから沈め折りします。
言いませんでしたが、上の沈め折りはopen sink でした。またカドの自由度がそのままになります。
一方 closed sink は紙を開かずに押し込めるように沈めます。
また、カドの自由度が下がります。
では実践へと移りましょう。
鶴の基本形まで折って下さい。
この後頭と尻尾になる部分を折り返して細くします。
今回はその部分を沈め折りに変えてみましょう。
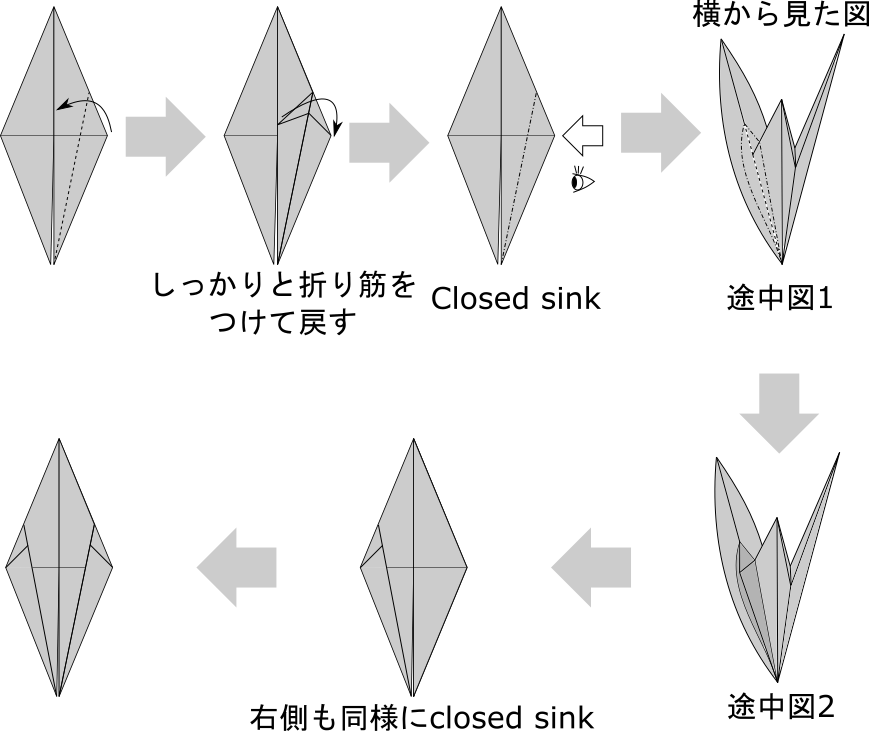
Closed sink はできるだけ開かずに内側に押し込んでしまいます。
なので、押し込んだ部分が多少汚くなってしまっても気にしないようにしましょう。
どうせ表には出てきませんし。
次は open sink です。Open sink は大きく開いて沈めます。
また、沈める部分の山谷がすべて反転する点も特徴的です。
わからなくなったときは途中図の山折り谷折りをしっかり確認しておりましょう。

さて closed sink と open sink 共にできたでしょうか。
出来ましたらそれを横から見てみてください。
右図のようになると思いますが、closed sink 側のほうがカドが open sink 側に比べ小さくなっていると思います。
これが先ほど述べました closed sink と open sink でのカドの自由度の違いです。closed sink では隣のカドの一部を巻き込むため、カドの自由度が下がってしまうのです。
closed sink 側

横から見た図
open sink 側
closed sink 側
open sink 側

樹形図
以上で基本的な折り方は完了です。
ここまでマスターできた方は間違いなく中級者から上級者への道を上っています。
折れない作品があってもあきらめずになんども挑戦してみてください。